Persamaan sekstik
Dalam aljabar, Polinomial sektik (atau hekik) adalah polinomial dari derajat enam. Persamaan sektik adalah persamaan polinomial berderajat enam — yaitu, persamaan yang sisi kiri adalah polinomial sextik dan sisi kanannya nol. Lebih tepatnya, itu berbentuk:
dimana a ≠ 0 dan koefisien a, b, c, d, e, f, g mungkin bilangan bulat, bilangan rasional, bilangan real, bilangan kompleks atau, lebih umum lagi, anggota dari bidang.
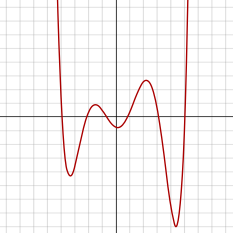
Fungsi sektik adalah fungsi yang ditentukan oleh polinomial sextik. Karena mereka memiliki derajat genap, fungsi sextik tampak mirip dengan fungsi kuartik saat dibuat grafik, kecuali fungsi tersebut memiliki tambahan maksimum lokal dan minimum lokal masing-masing. Turunan dari fungsi sextic adalah fungsi kuintik.
Karena fungsi sektik didefinisikan oleh polinomial dengan derajat genap, ia memiliki batas tak hingga yang sama ketika argumennya menjadi positif atau negatif tak hingga. Jika koefisien awal a positif, maka fungsinya meningkat menjadi positif tak terhingga di kedua sisi dan dengan demikian fungsinya memiliki minimum global. Demikian juga, jika a negatif, fungsi sextic berkurang hingga negatif tak terhingga dan memiliki maksimum global.
Beberapa persamaan derajat keenam, seperti ax6 + dx3 + g = 0, dapat diselesaikan dengan memfaktorkan menjadi radikal, tetapi sextics lainnya tidak bisa. Évariste Galois mengembangkan teknik untuk menentukan apakah suatu persamaan dapat diselesaikan dengan radikal yang memunculkan bidang teori Galois.[1]
Ini mengikuti dari teori Galois bahwa persamaan sextic dapat diselesaikan dalam istilah radikal jika dan hanya jika kelompok Galois mengandung salah satu dalam grup orde 48 yang menstabilkan partisi himpunan akar menjadi tiga himpunan bagian dari dua akar atau dalam kelompok ordo 72 yang menstabilkan sekat dari himpunan akar menjadi dua himpunan bagian dari tiga akar.
Ada rumus untuk menguji kedua kasus tersebut, dan, jika persamaan tersebut dapat dipecahkan, hitung akarnya dalam akar.[2]
Persamaan sextic umum dapat diselesaikan dengan menggunakan Fungsi Kampé de Fériet.[1] Kelas sextik yang lebih terbatas dapat diselesaikan dalam istilah fungsi hipergeometrik umum dalam satu variabel menggunakan pendekatan Felix Klein untuk menyelesaikan persamaan kuintik.[1]
Lihat pula
suntingReferensi
sunting- ^ a b c Mathworld - Sextic Equation
- ^ T. R. Hagedorn, General formulas for solving solvable sextic equations, J. Algebra 233 (2000), 704-757
