Wikipedia

Grup titik

grup geometris simetri (isometri) yang menjaga setidaknya satu titik tetap

Bauhinia blakeana bunga di bendera wilayah Hong Kong memiliki simetri C 5 ; bintang di setiap kelopak memiliki simetri D 5 .
Yin dan Yang simbol memiliki geometri simetri C 2 dengan warna terbalik

Dalam geometri, grup titik adalah grup geometris simetri (isometri) yang menjaga setidaknya satu titik tetap. Kelompok titik dapat ada dalam ruang Euklides dengan dimensi apa pun, dan setiap kelompok titik dalam dimensi d adalah subkelompok dari grup ortogonal O(d). Kelompok titik dapat direalisasikan sebagai himpunan matriks ortogonal M yang mengubah titik x menjadi titik y :

y = Mx

dimana asal adalah titik tetap. Elemen kelompok titik dapat berupa rotasi (determinan dari M = 1) atau yang lain refleksi, atau rotasi tidak tepat (determinan dari M = −1).

Kelompok titik diskrit di lebih dari satu dimensi datang dalam keluarga tak berhingga, tetapi dari teorema pembatasan kristalografi dan salah satu teorema Bieberbach. setiap jumlah dimensi hanya memiliki jumlah terbatas dari kelompok titik yang simetris di beberapa kisi atau kisi dengan nomor itu. Ini adalah grup titik kristalografi.

Grup titik kiral dan akiral, grup refleksi sunting

Kelompok titik dapat diklasifikasikan ke dalam kelompok kiral (atau rotasi murni) dan kelompok akiral .[1] Gugus kiral adalah subgrup dari grup ortogonal khusus SO( d ): grup ini hanya berisi transformasi ortogonal yang mempertahankan orientasi, yaitu, determinan +1. Gugus akiral juga mengandung transformasi determinan −1. Dalam gugus akiral, transformasi yang mempertahankan orientasi membentuk subgrup (kiral) dari indeks 2.

Grup Coxeter Hingga atau kelompok refleksi adalah kelompok titik yang dihasilkan murni oleh sekumpulan cermin pantul yang melewati titik yang sama. Grup peringkat n Coxeter memiliki mirror n dan diwakili oleh diagram Coxeter-Dynkin. Notasi Coxeter menawarkan notasi tanda kurung yang setara dengan diagram Coxeter, dengan simbol markup untuk rotasi dan grup titik subsimetri lainnya. Kelompok refleksi harus akiral (kecuali untuk grup trivial yang hanya mengandung elemen identitas).

Daftar grup titik sunting

Satu dimensi sunting

Hanya ada dua grup titik satu dimensi, yaitu grup identitas dan kelompok refleksi.

Group Coxeter Diagram Coxeter Urutan Deskripsi
C1 [ ]+ 1 Identity
D1 [ ] 2 Reflection group

Dua dimensi sunting

Grup titik dalam dua dimensi, terkadang disebut grup roset.

Mereka datang dalam dua keluarga yang tidak terbatas:

  1. Grup siklik Cn of n - grup rotasi lipat
  2. Grup dihedral Dn of n-kelompok rotasi dan refleksi lipat

Menerapkan teorema pembatasan kristalografi membatasi n ke nilai 1, 2, 3, 4, dan 6 untuk kedua famili, menghasilkan 10 kelompok.

Grup Intl Orbifold Coxeter Urutan Deskripsi
Cn n n• [n]+ n Siklik: n - rotasi lipat. Grup abstrak Z n , grup bilangan bulat di bawah penambahan modulo n .
Dn nm *n• [n] 2n Dihedral: siklik dengan refleksi. Grup abstrak Dihn, grup dihedral.
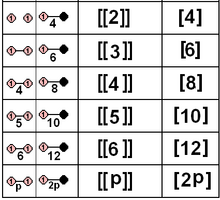
Isomorfisme hingga dan korespondensi

Himpunan bagian dari grup titik pantulan murni, yang ditentukan oleh 1 atau 2 mirror, juga dapat diberikan oleh grup Coxeter dan poligon terkait. Ini termasuk 5 kelompok kristalografi. Simetri kelompok pantulan dapat digandakan dengan isomorphism, memetakan kedua cermin satu sama lain dengan cermin membagi dua, menggandakan simetri.

Reflektif Rotasi Terkait
poligon
Group Grup Coxeter Diagram Coxeter Urutan Subgrup Coxeter Urutan
D1 A1 [ ] 2 C1 []+ 1 Digon
D2 A12 [2] 4 C2 [2]+ 2 Persegi panjang
D3 A2 [3] 6 C3 [3]+ 3 Segitiga sama sisi
D4 BC2 [4] 8 C4 [4]+ 4 Persegi
D5 H2 [5] 10 C5 [5]+ 5 Segi lima biasa
D6 G2 [6] 12 C6 [6]+ 6 Segi enam biasa
Dn I2(n) [n] 2n Cn [n]+ n Poligon beraturan
D2×2 A12×2 [[2]] = [4] = 8
D3×2 A2×2 [[3]] = [6] = 12
D4×2 BC2×2 [[4]] = [8] = 16
D5×2 H2×2 [[5]] = [10] = 20
D6×2 G2×2 [[6]] = [12] = 24
Dn×2 I2(n)×2 [[n]] = [2n] = 4n

Tiga dimensi sunting

Artikel utama: Grup titik dalam tiga dimensi

Grup titik dalam tiga dimensi, kadang disebut grup titik molekul setelah digunakan secara luas dalam mempelajari kesimetrian molekul kecil.

Mereka datang dalam 7 kelompok tak terbatas dari kelompok aksial atau prismatik, dan 7 kelompok polihedral atau Platonis tambahan. Dalam Notasi Schönflies, *

  • Grup aksial: Cn, S2n, Cnh, Cnv, Dn, Dnd, Dnh
  • Grup polihedral: T, Td, Th, O, Oh, I, Ih

Menerapkan teorema pembatasan kristalografi ke grup ini menghasilkan 32 grup titik kristalografi.

Domain fundamental berwarna genap/ganjil dari grup reflektif
C1v
Urutan 2 		C2v
Urutan 4 		C3v
Urutan 6 		C4v
Urutan 8 		C5v
Urutan 10 		C6v
Urutan 12 		...
D1h
Urutan 4 		D2h
Urutan 8 		D3h
Urutan 12 		D4h
Urutan 16 		D5h
Urutan 20 		D6h
Urutan 24 		...
Td
Urutan 24 		Oh
Urutan 48 		Ih
Urutan 120
[[Notasi Hermann–Mauguin|Intl]* Geo
[2] 		Orbifold Schönflies Conway Coxeter Urutan
1 1 1 C1 C1 [ ]+ 1
1 22 ×1 Ci = S2 CC2 [2+,2+] 2
2 = m 1 *1 Cs = C1v = C1h ±C1 = CD2 [ ] 2
2
3
4
5
6
n 		2
3
4
5
6
n 		22
33
44
55
66
nn 		C2
C3
C4
C5
C6
Cn 		C2
C3
C4
C5
C6
Cn 		[2]+
[3]+
[4]+
[5]+
[6]+
[n]+
 2
3
4
5
6
n
mm2
3m
4mm
5m
6mm
nmm
nm 		2
3
4
5
6
n 		*22
*33
*44
*55
*66
*nn 		C2v
C3v
C4v
C5v
C6v
Cnv 		CD4
CD6
CD8
CD10
CD12
CD2n 		[2]
[3]
[4]
[5]
[6]
[n] 		4
6
8
10
12
2n
2/m
6
4/m
10
6/m
n/m
2n 		2 2
3 2
4 2
5 2
6 2
n 2 		2*
3*
4*
5*
6*
n* 		C2h
C3h
C4h
C5h
C6h
Cnh 		±C2
CC6
±C4
CC10
±C6
±Cn / CC2n 		[2,2+]
[2,3+]
[2,4+]
[2,5+]
[2,6+]
[2,n+] 		4
6
8
10
12
2n
4
3
8
5
12
2n
n 		4 2
6 2
8 2
10 2
12 2
2n 2 		2×
3×
4×
5×
6×
n× 		S4
S6
S8
S10
S12
S2n 		CC4
±C3
CC8
±C5
CC12
CC2n / ±Cn 		[2+,4+]
[2+,6+]
[2+,8+]
[2+,10+]
[2+,12+]
[2+,2n+] 		4
6
8
10
12
2n
Intl Geo Intl Geo Orbifold Schönflies Conway Coxeter Urutan
222
32
422
52
622
n22
n2 		2 2
3 2
4 2
5 2
6 2
n 2 		222
223
224
225
226
22n 		D2
D3
D4
D5
D6
Dn 		D4
D6
D8
D10
D12
D2n 		[2,2]+
[2,3]+
[2,4]+
[2,5]+
[2,6]+
[2,n]+ 		4
6
8
10
12
2n
mmm
6m2
4/mmm
10m2
6/mmm
n/mmm
2nm2 		2 2
3 2
4 2
5 2
6 2
n 2 		*222
*223
*224
*225
*226
*22n 		D2h
D3h
D4h
D5h
D6h
Dnh 		±D4
DD12
±D8
DD20
±D12
±D2n / DD4n 		[2,2]
[2,3]
[2,4]
[2,5]
[2,6]
[2,n] 		8
12
16
20
24
4n
42m
3m
82m
5m
122m
2n2m
nm 		4 2
6 2
8 2
10 2
12 2
n 2
 2*2
2*3
2*4
2*5
2*6
2*n 		D2d
D3d
D4d
D5d
D6d
Dnd 		±D4
±D6
DD16
±D10
DD24
DD4n / ±D2n 		[2+,4]
[2+,6]
[2+,8]
[2+,10]
[2+,12]
[2+,2n] 		8
12
16
20
24
4n
23 3 3 332 T T [3,3]+ 12
m3 4 3 3*2 Th ±T [3+,4] 24
43m 3 3 *332 Td TO [3,3] 24
432 4 3 432 O O [3,4]+ 24
m3m 4 3 *432 Oh ±O [3,4] 48
532 5 3 532 I I [3,5]+ 60
53m 5 3 *532 Ih ±I [3,5] 120
(*) Ketika entri Intl digandakan, yang pertama untuk genap n , yang kedua untuk ganjil n .

Grup refleksi sunting

Isomorfisme hingga dan korespondensi

Kelompok titik refleksi, ditentukan oleh 1 sampai 3 bidang cermin, juga dapat diberikan oleh grup Coxeter dan polihedra terkait. Grup [3,3] dapat digandakan, ditulis sebagai [[ 3,3]], memetakan cermin pertama dan terakhir satu sama lain, menggandakan simetri menjadi 48, dan isomorfik ke grup [4,3].

Schönflies grup Coxeter Diagram Coxeter Urutan Terkait reguler dan
Td A3 [3,3] 24 Tetrahedron
Td×Dih1 = Oh A3×2 = BC3 [[3,3]] = [4,3] = 48 Oktahedron bintang
Oh BC3 [4,3] 48 kubus, segi delapan
Ih H3 [5,3] 120 Icosahedron, dodecahedron
D3h A2×A1 [3,2] 12 Prisma segitiga
D3h×Dih1 = D6h A2×A1×2 [[3],2] = 24 Prisma segi enam
D4h BC2×A1 [4,2] 16 Prisma persegi
D4h×Dih1 = D8h BC2×A1×2 [[4],2] = [8,2] = 32 Octagonal prism
D5h H2×A1 [5,2] 20 Prisma segi lima
D6h G2×A1 [6,2] 24 Prisma segi enam
Dnh I2(n)×A1 [n,2] 4n n-gonal prisma
Dnh×Dih1 = D2nh I2(n)×A1×2 [[n],2] = 8n
D2h A13 [2,2] 8 Balok
D2h×Dih1 A13×2 [[2],2] = [4,2] = 16
D2h×Dih3 = Oh A13×6 [3[2,2]] = [4,3] = 48
C3v A2 [1,3] 6 Hosohedron
C4v BC2 [1,4] 8
C5v H2 [1,5] 10
C6v G2 [1,6] 12
Cnv I2(n) [1,n] 2n
Cnv×Dih1 = C2nv I2(n)×2 [1,[n]] = [1,2n] = 4n
C2v A12 [1,2] 4
C2v×Dih1 A12×2 [1,[2]] = 8
Cs A1 [1,1] 2

Four dimensions sunting

Artikel utama: Point groups in four dimensions

The four-dimensional point groups (chiral as well as achiral) are listed in Conway and Smith,[1] Section 4, Tables 4.1-4.3.

Finite isomorphism and correspondences

The following list gives the four-dimensional reflection groups (excluding those that leave a subspace fixed and that are therefore lower-dimensional reflection groups). Each group is specified as a Coxeter group, and like the polyhedral groups of 3D, it can be named by its related convex regular 4-polytope. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example [3,3,3]+ has three 3-fold gyration points and symmetry order 60. Front-back symmetric groups like [3,3,3] and [3,4,3] can be doubled, shown as double brackets in Coxeter's notation, for example [[3,3,3]] with its order doubled to 240.

Coxeter group/notation Coxeter diagram Order Related polytopes
A4 [3,3,3] 120 5-cell
A4×2 [[3,3,3]] 240 5-cell dual compound
BC4 [4,3,3] 384 16-cell/Tesseract
D4 [31,1,1] 192 Demitesseractic
D4×2 = BC4 <[3,31,1]> = [4,3,3] = 384
D4×6 = F4 [3[31,1,1]] = [3,4,3] = 1152
F4 [3,4,3] 1152 24-cell
F4×2 [[3,4,3]] 2304 24-cell dual compound
H4 [5,3,3] 14400 120-cell/600-cell
A3×A1 [3,3,2] 48 Tetrahedral prism
A3×A1×2 [[3,3],2] = [4,3,2] = 96 Octahedral prism
BC3×A1 [4,3,2] 96
H3×A1 [5,3,2] 240 Icosahedral prism
A2×A2 [3,2,3] 36 Duoprism
A2×BC2 [3,2,4] 48
A2×H2 [3,2,5] 60
A2×G2 [3,2,6] 72
BC2×BC2 [4,2,4] 64
BC22×2 [[4,2,4]] 128
BC2×H2 [4,2,5] 80
BC2×G2 [4,2,6] 96
H2×H2 [5,2,5] 100
H2×G2 [5,2,6] 120
G2×G2 [6,2,6] 144
I2(p)×I2(q) [p,2,q] 4pq
I2(2p)×I2(q) [[p],2,q] = [2p,2,q] = 8pq
I2(2p)×I2(2q) [[p]],2,[[q]] = [2p,2,2q] = 16pq
I2(p)2×2 [[p,2,p]] 8p2
I2(2p)2×2 [[[p],2,[p]]] = [[2p,2,2p]] = 32p2
A2×A1×A1 [3,2,2] 24
BC2×A1×A1 [4,2,2] 32
H2×A1×A1 [5,2,2] 40
G2×A1×A1 [6,2,2] 48
I2(p)×A1×A1 [p,2,2] 8p
I2(2p)×A1×A1×2 [[p],2,2] = [2p,2,2] = 16p
I2(p)×A12×2 [p,2,[2]] = [p,2,4] = 16p
I2(2p)×A12×4 [[p]],2,[[2]] = [2p,2,4] = 32p
A1×A1×A1×A1 [2,2,2] 16 4-orthotope
A12×A1×A1×2 [[2],2,2] = [4,2,2] = 32
A12×A12×4 [[2]],2,[[2]] = [4,2,4] = 64
A13×A1×6 [3[2,2],2] = [4,3,2] = 96
A14×24 [3,3[2,2,2]] = [4,3,3] = 384

Five dimensions sunting

Finite isomorphism and correspondences

The following table gives the five-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example [3,3,3,3]+ has four 3-fold gyration points and symmetry order 360.

Coxeter group/notation Coxeter
diagrams 		Order Related regular and
prismatic polytopes
A5 [3,3,3,3] 720 5-simplex
A5×2 [[3,3,3,3]] 1440 5-simplex dual compound
BC5 [4,3,3,3] 3840 5-cube, 5-orthoplex
D5 [32,1,1] 1920 5-demicube
D5×2 <[3,3,31,1]> = 3840
A4×A1 [3,3,3,2] 240 5-cell prism
A4×A1×2 [[3,3,3],2] 480
BC4×A1 [4,3,3,2] 768 tesseract prism
F4×A1 [3,4,3,2] 2304 24-cell prism
F4×A1×2 [[3,4,3],2] 4608
H4×A1 [5,3,3,2] 28800 600-cell or 120-cell prism
D4×A1 [31,1,1,2] 384 Demitesseract prism
A3×A2 [3,3,2,3] 144 Duoprism
A3×A2×2 [[3,3],2,3] 288
A3×BC2 [3,3,2,4] 192
A3×H2 [3,3,2,5] 240
A3×G2 [3,3,2,6] 288
A3×I2(p) [3,3,2,p] 48p
BC3×A2 [4,3,2,3] 288
BC3×BC2 [4,3,2,4] 384
BC3×H2 [4,3,2,5] 480
BC3×G2 [4,3,2,6] 576
BC3×I2(p) [4,3,2,p] 96p
H3×A2 [5,3,2,3] 720
H3×BC2 [5,3,2,4] 960
H3×H2 [5,3,2,5] 1200
H3×G2 [5,3,2,6] 1440
H3×I2(p) [5,3,2,p] 240p
A3×A12 [3,3,2,2] 96
BC3×A12 [4,3,2,2] 192
H3×A12 [5,3,2,2] 480
A22×A1 [3,2,3,2] 72 duoprism prism
A2×BC2×A1 [3,2,4,2] 96
A2×H2×A1 [3,2,5,2] 120
A2×G2×A1 [3,2,6,2] 144
BC22×A1 [4,2,4,2] 128
BC2×H2×A1 [4,2,5,2] 160
BC2×G2×A1 [4,2,6,2] 192
H22×A1 [5,2,5,2] 200
H2×G2×A1 [5,2,6,2] 240
G22×A1 [6,2,6,2] 288
I2(p)×I2(q)×A1 [p,2,q,2] 8pq
A2×A13 [3,2,2,2] 48
BC2×A13 [4,2,2,2] 64
H2×A13 [5,2,2,2] 80
G2×A13 [6,2,2,2] 96
I2(p)×A13 [p,2,2,2] 16p
A15 [2,2,2,2] 32 5-orthotope
A15×(2!) [[2],2,2,2] = 64
A15×(2!×2!) [[2]],2,[2],2] = 128
A15×(3!) [3[2,2],2,2] = 192
A15×(3!×2!) [3[2,2],2,[[2]] = 384
A15×(4!) [3,3[2,2,2],2]] = 768
A15×(5!) [3,3,3[2,2,2,2]] = 3840

Six dimensions sunting

Finite isomorphism and correspondences

The following table gives the six-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related pure rotational groups exist for each with half the order, and can be represented by the bracket Coxeter notation with a '+' exponent, for example [3,3,3,3,3]+ has five 3-fold gyration points and symmetry order 2520.

Coxeter group Coxeter
diagram 		Order Related regular and
prismatic polytopes
A6 [3,3,3,3,3] 5040 (7!) 6-simplex
A6×2 [[3,3,3,3,3]] 10080 (2×7!) 6-simplex dual compound
BC6 [4,3,3,3,3] 46080 (26×6!) 6-cube, 6-orthoplex
D6 [3,3,3,31,1] 23040 (25×6!) 6-demicube
E6 [3,32,2] 51840 (72×6!) 122, 221
A5×A1 [3,3,3,3,2] 1440 (2×6!) 5-simplex prism
BC5×A1 [4,3,3,3,2] 7680 (26×5!) 5-cube prism
D5×A1 [3,3,31,1,2] 3840 (25×5!) 5-demicube prism
A4×I2(p) [3,3,3,2,p] 240p Duoprism
BC4×I2(p) [4,3,3,2,p] 768p
F4×I2(p) [3,4,3,2,p] 2304p
H4×I2(p) [5,3,3,2,p] 28800p
D4×I2(p) [3,31,1,2,p] 384p
A4×A12 [3,3,3,2,2] 480
BC4×A12 [4,3,3,2,2] 1536
F4×A12 [3,4,3,2,2] 4608
H4×A12 [5,3,3,2,2] 57600
D4×A12 [3,31,1,2,2] 768
A32 [3,3,2,3,3] 576
A3×BC3 [3,3,2,4,3] 1152
A3×H3 [3,3,2,5,3] 2880
BC32 [4,3,2,4,3] 2304
BC3×H3 [4,3,2,5,3] 5760
H32 [5,3,2,5,3] 14400
A3×I2(p)×A1 [3,3,2,p,2] 96p Duoprism prism
BC3×I2(p)×A1 [4,3,2,p,2] 192p
H3×I2(p)×A1 [5,3,2,p,2] 480p
A3×A13 [3,3,2,2,2] 192
BC3×A13 [4,3,2,2,2] 384
H3×A13 [5,3,2,2,2] 960
I2(p)×I2(q)×I2(r) [p,2,q,2,r] 8pqr Triaprism
I2(p)×I2(q)×A12 [p,2,q,2,2] 16pq
I2(p)×A14 [p,2,2,2,2] 32p
A16 [2,2,2,2,2] 64 6-orthotope

Seven dimensions sunting

The following table gives the seven-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, defined by an even number of reflections, and can be represented by the bracket Coxeter notation with a '+' exponent, for example [3,3,3,3,3,3]+ has six 3-fold gyration points and symmetry order 20160.

Coxeter group Coxeter diagram Order Related polytopes
A7 [3,3,3,3,3,3] 40320 (8!) 7-simplex
A7×2 [[3,3,3,3,3,3]] 80640 (2×8!) 7-simplex dual compound
BC7 [4,3,3,3,3,3] 645120 (27×7!) 7-cube, 7-orthoplex
D7 [3,3,3,3,31,1] 322560 (26×7!) 7-demicube
E7 [3,3,3,32,1] 2903040 (8×9!) 321, 231, 132
A6×A1 [3,3,3,3,3,2] 10080 (2×7!)
BC6×A1 [4,3,3,3,3,2] 92160 (27×6!)
D6×A1 [3,3,3,31,1,2] 46080 (26×6!)
E6×A1 [3,3,32,1,2] 103680 (144×6!)
A5×I2(p) [3,3,3,3,2,p] 1440p
BC5×I2(p) [4,3,3,3,2,p] 7680p
D5×I2(p) [3,3,31,1,2,p] 3840p
A5×A12 [3,3,3,3,2,2] 2880
BC5×A12 [4,3,3,3,2,2] 15360
D5×A12 [3,3,31,1,2,2] 7680
A4×A3 [3,3,3,2,3,3] 2880
A4×BC3 [3,3,3,2,4,3] 5760
A4×H3 [3,3,3,2,5,3] 14400
BC4×A3 [4,3,3,2,3,3] 9216
BC4×BC3 [4,3,3,2,4,3] 18432
BC4×H3 [4,3,3,2,5,3] 46080
H4×A3 [5,3,3,2,3,3] 345600
H4×BC3 [5,3,3,2,4,3] 691200
H4×H3 [5,3,3,2,5,3] 1728000
F4×A3 [3,4,3,2,3,3] 27648
F4×BC3 [3,4,3,2,4,3] 55296
F4×H3 [3,4,3,2,5,3] 138240
D4×A3 [31,1,1,2,3,3] 4608
D4×BC3 [3,31,1,2,4,3] 9216
D4×H3 [3,31,1,2,5,3] 23040
A4×I2(p)×A1 [3,3,3,2,p,2] 480p
BC4×I2(p)×A1 [4,3,3,2,p,2] 1536p
D4×I2(p)×A1 [3,31,1,2,p,2] 768p
F4×I2(p)×A1 [3,4,3,2,p,2] 4608p
H4×I2(p)×A1 [5,3,3,2,p,2] 57600p
A4×A13 [3,3,3,2,2,2] 960
BC4×A13 [4,3,3,2,2,2] 3072
F4×A13 [3,4,3,2,2,2] 9216
H4×A13 [5,3,3,2,2,2] 115200
D4×A13 [3,31,1,2,2,2] 1536
A32×A1 [3,3,2,3,3,2] 1152
A3×BC3×A1 [3,3,2,4,3,2] 2304
A3×H3×A1 [3,3,2,5,3,2] 5760
BC32×A1 [4,3,2,4,3,2] 4608
BC3×H3×A1 [4,3,2,5,3,2] 11520
H32×A1 [5,3,2,5,3,2] 28800
A3×I2(p)×I2(q) [3,3,2,p,2,q] 96pq
BC3×I2(p)×I2(q) [4,3,2,p,2,q] 192pq
H3×I2(p)×I2(q) [5,3,2,p,2,q] 480pq
A3×I2(p)×A12 [3,3,2,p,2,2] 192p
BC3×I2(p)×A12 [4,3,2,p,2,2] 384p
H3×I2(p)×A12 [5,3,2,p,2,2] 960p
A3×A14 [3,3,2,2,2,2] 384
BC3×A14 [4,3,2,2,2,2] 768
H3×A14 [5,3,2,2,2,2] 1920
I2(p)×I2(q)×I2(r)×A1 [p,2,q,2,r,2] 16pqr
I2(p)×I2(q)×A13 [p,2,q,2,2,2] 32pq
I2(p)×A15 [p,2,2,2,2,2] 64p
A17 [2,2,2,2,2,2] 128

Eight dimensions sunting

The following table gives the eight-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, defined by an even number of reflections, and can be represented by the bracket Coxeter notation with a '+' exponent, for example [3,3,3,3,3,3,3]+ has seven 3-fold gyration points and symmetry order 181440.

Coxeter group Coxeter diagram Order Related polytopes
A8 [3,3,3,3,3,3,3] 362880 (9!) 8-simplex
A8×2 [[3,3,3,3,3,3,3]] 725760 (2×9!) 8-simplex dual compound
BC8 [4,3,3,3,3,3,3] 10321920 (288!) 8-cube,8-orthoplex
D8 [3,3,3,3,3,31,1] 5160960 (278!) 8-demicube
E8 [3,3,3,3,32,1] 696729600 (192×10!) 421, 241, 142
A7×A1 [3,3,3,3,3,3,2] 80640 7-simplex prism
BC7×A1 [4,3,3,3,3,3,2] 645120 7-cube prism
D7×A1 [3,3,3,3,31,1,2] 322560 7-demicube prism
E7×A1 [3,3,3,32,1,2] 5806080 321 prism, 231 prism, 142 prism
A6×I2(p) [3,3,3,3,3,2,p] 10080p duoprism
BC6×I2(p) [4,3,3,3,3,2,p] 92160p
D6×I2(p) [3,3,3,31,1,2,p] 46080p
E6×I2(p) [3,3,32,1,2,p] 103680p
A6×A12 [3,3,3,3,3,2,2] 20160
BC6×A12 [4,3,3,3,3,2,2] 184320
D6×A12 [33,1,1,2,2] 92160
E6×A12 [3,3,32,1,2,2] 207360
A5×A3 [3,3,3,3,2,3,3] 17280
BC5×A3 [4,3,3,3,2,3,3] 92160
D5×A3 [32,1,1,2,3,3] 46080
A5×BC3 [3,3,3,3,2,4,3] 34560
BC5×BC3 [4,3,3,3,2,4,3] 184320
D5×BC3 [32,1,1,2,4,3] 92160
A5×H3 [3,3,3,3,2,5,3]
BC5×H3 [4,3,3,3,2,5,3]
D5×H3 [32,1,1,2,5,3]
A5×I2(p)×A1 [3,3,3,3,2,p,2]
BC5×I2(p)×A1 [4,3,3,3,2,p,2]
D5×I2(p)×A1 [32,1,1,2,p,2]
A5×A13 [3,3,3,3,2,2,2]
BC5×A13 [4,3,3,3,2,2,2]
D5×A13 [32,1,1,2,2,2]
A4×A4 [3,3,3,2,3,3,3]
BC4×A4 [4,3,3,2,3,3,3]
D4×A4 [31,1,1,2,3,3,3]
F4×A4 [3,4,3,2,3,3,3]
H4×A4 [5,3,3,2,3,3,3]
BC4×BC4 [4,3,3,2,4,3,3]
D4×BC4 [31,1,1,2,4,3,3]
F4×BC4 [3,4,3,2,4,3,3]
H4×BC4 [5,3,3,2,4,3,3]
D4×D4 [31,1,1,2,31,1,1]
F4×D4 [3,4,3,2,31,1,1]
H4×D4 [5,3,3,2,31,1,1]
F4×F4 [3,4,3,2,3,4,3]
H4×F4 [5,3,3,2,3,4,3]
H4×H4 [5,3,3,2,5,3,3]
A4×A3×A1 [3,3,3,2,3,3,2] duoprism prisms
A4×BC3×A1 [3,3,3,2,4,3,2]
A4×H3×A1 [3,3,3,2,5,3,2]
BC4×A3×A1 [4,3,3,2,3,3,2]
BC4×BC3×A1 [4,3,3,2,4,3,2]
BC4×H3×A1 [4,3,3,2,5,3,2]
H4×A3×A1 [5,3,3,2,3,3,2]
H4×BC3×A1 [5,3,3,2,4,3,2]
H4×H3×A1 [5,3,3,2,5,3,2]
F4×A3×A1 [3,4,3,2,3,3,2]
F4×BC3×A1 [3,4,3,2,4,3,2]
F4×H3×A1 [3,4,2,3,5,3,2]
D4×A3×A1 [31,1,1,2,3,3,2]
D4×BC3×A1 [31,1,1,2,4,3,2]
D4×H3×A1 [31,1,1,2,5,3,2]
A4×I2(p)×I2(q) [3,3,3,2,p,2,q] triaprism
BC4×I2(p)×I2(q) [4,3,3,2,p,2,q]
F4×I2(p)×I2(q) [3,4,3,2,p,2,q]
H4×I2(p)×I2(q) [5,3,3,2,p,2,q]
D4×I2(p)×I2(q) [31,1,1,2,p,2,q]
A4×I2(p)×A12 [3,3,3,2,p,2,2]
BC4×I2(p)×A12 [4,3,3,2,p,2,2]
F4×I2(p)×A12 [3,4,3,2,p,2,2]
H4×I2(p)×A12 [5,3,3,2,p,2,2]
D4×I2(p)×A12 [31,1,1,2,p,2,2]
A4×A14 [3,3,3,2,2,2,2]
BC4×A14 [4,3,3,2,2,2,2]
F4×A14 [3,4,3,2,2,2,2]
H4×A14 [5,3,3,2,2,2,2]
D4×A14 [31,1,1,2,2,2,2]
A3×A3×I2(p) [3,3,2,3,3,2,p]
BC3×A3×I2(p) [4,3,2,3,3,2,p]
H3×A3×I2(p) [5,3,2,3,3,2,p]
BC3×BC3×I2(p) [4,3,2,4,3,2,p]
H3×BC3×I2(p) [5,3,2,4,3,2,p]
H3×H3×I2(p) [5,3,2,5,3,2,p]
A3×A3×A12 [3,3,2,3,3,2,2]
BC3×A3×A12 [4,3,2,3,3,2,2]
H3×A3×A12 [5,3,2,3,3,2,2]
BC3×BC3×A12 [4,3,2,4,3,2,2]
H3×BC3×A12 [5,3,2,4,3,2,2]
H3×H3×A12 [5,3,2,5,3,2,2]
A3×I2(p)×I2(q)×A1 [3,3,2,p,2,q,2]
BC3×I2(p)×I2(q)×A1 [4,3,2,p,2,q,2]
H3×I2(p)×I2(q)×A1 [5,3,2,p,2,q,2]
A3×I2(p)×A13 [3,3,2,p,2,2,2]
BC3×I2(p)×A13 [4,3,2,p,2,2,2]
H3×I2(p)×A13 [5,3,2,p,2,2,2]
A3×A15 [3,3,2,2,2,2,2]
BC3×A15 [4,3,2,2,2,2,2]
H3×A15 [5,3,2,2,2,2,2]
I2(p)×I2(q)×I2(r)×I2(s) [p,2,q,2,r,2,s] 16pqrs
I2(p)×I2(q)×I2(r)×A12 [p,2,q,2,r,2,2] 32pqr
I2(p)×I2(q)×A14 [p,2,q,2,2,2,2] 64pq
I2(p)×A16 [p,2,2,2,2,2,2] 128p
A18 [2,2,2,2,2,2,2] 256

Lihat pula sunting

Referensi sunting

  1. ^ a b Conway, John H.; Smith, Derek A. (2003). On quaternions and octonions: their geometry, arithmetic, and symmetry. A K Peters. ISBN 978-1-56881-134-5. 
  2. ^ Grup Ruang Kristalografi dalam aljabar geometris, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF [1] Diarsipkan 2020-10-20 di Wayback Machine.
  • H. S. M. Coxeter: Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2] Diarsipkan 2016-07-11 di Wayback Machine.
    • (Paper 23) H. S. M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
  • H. S. M. Coxeter and W. O. J. Moser. Generators and Relations for Discrete Groups 4th ed, Springer-Verlag. New York. 1980
  • N. W. Johnson: Geometries and Transformations, (2018) Chapter 11: Finite symmetry groups

Pranala luar sunting

Diperoleh dari "https://id.wikipedia.org/w/index.php?title=Grup_titik&oldid=23984166"